Cross Diagonal Cover - III

I found many counterexamples to my conjecture, like

• for Case 2 in 7 by 5 grid we have 12, 11 by 5 grid we have 19 and 15 by 5 grid we have 26 filled squares
• for Case 3 in 4 by 10 grid we have 10 filled squares

Also, grant93jr made the following comment:

Therefore (s)he proved the follwing statement:

Given $m>n$, whenever $n-1$ divides $m-1$ we have $m$ filled squares.

Examples of such grids are: 3 by 5, 4 by 7, 4 by 10, ….

In this comment grant93jr also suggested that the algorithm terminates after $k(m-1) = l(n-1)$ steps where $k, l$ are some natural numbers. It is certainly true, but I haven’t been able to use this idea for counting number of filled squares when $n-1$ does not divide $m-1$ since in that case some squares are filled twice.

There is another unexplained observation:

Why no filled square has more than 2 crosses?

Frustrated by so many unanswered questions I started colouring squares, so that number of times I visited a square is not visible. Since I really don’t care about how many times I visited given square while counting the number of filled squares this may help in understanding the underlying symmetry.

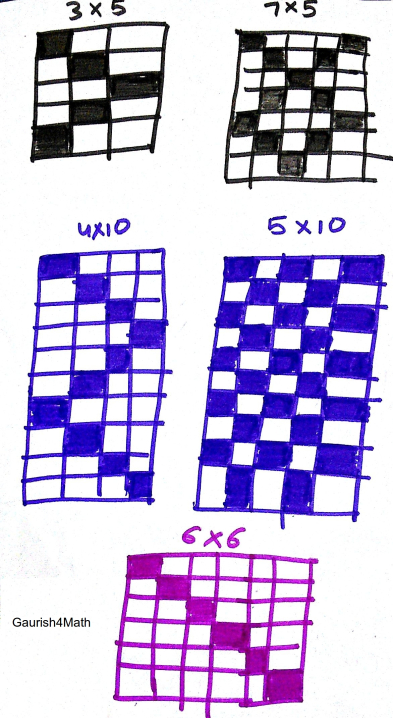
After observing above diagrams I suspect that my algorithm leads to a non-deterministic cellular automata.

So, the question which still remains to be answered is:

How many filled squares are there when $m>n$ and $n-1$ does not divide $m-1$ ?

Examples of such grids are: 7 by 5, 11 by 5, 15 by 5 …