Cross Diagonal Cover - V

This has been an exciting week! Prof. Sukanta Pati proved an interesting theorem that enables us to get decomposition of $2m-1\times n$ grids into simpler grids, hence simplifying counting to large extent (note that $m=n$ is also allowed). It enables us to surpass the difficulty posed by “more than two crosses in one square”, thus supporting the idea of colouring (i.e. not giving importance to two crosses in a square).

Given $m\times n$ grid which has consisting of $m$ rows and $n$ columns such that the terminating corner square lie in $m^{th}$ row. Let the number of covered squares in $m\times n$ grid be $C(m,n)$ . Then for $2m-1\times n$ grid we have $C(2m-1, n)= 2C(m,n)-\beta(m,n)$ where $\beta(m,n)$ is the number of covered squares in $m^{th}$ row of $m\times n$ grid.

Instead of giving its proof, I will give an example when $m=5, n=10$.

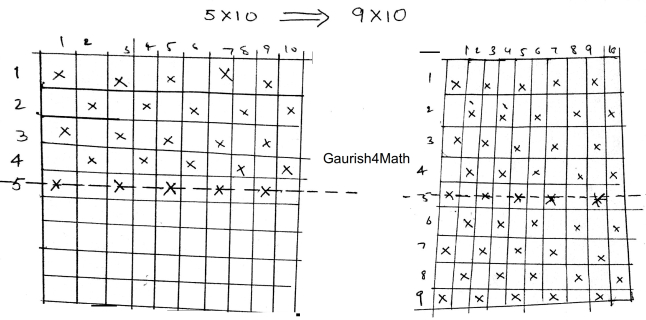
Here, $C(5,10) = 25$ and $C(9,10) = 2\times 25 - 5 = 45$. Using this example you can easily prove the generalized statement by exploiting the bilateral symmetry of grid and crosses (x) about the dotted line.

Though I suspected that the least common multiple of $m-1, n-1$ determine the number of steps my algorithm evaluates, Pritam Laskar found the exact formula.

Given a $m\times n$ grid, the Cross Diagonal Cover algorithm terminates after $lcm(m-1, n-1) + 1$ steps.

For proof, follow the arguments of grant93jr in his/her comment (he/she mistakenly called their lcm to be their gcd).

Using the SageMath Program, about which I wrote in previous post, I am pretty sure that $\gcd(m,n)$ always divides the number of filled squares. So, now the question is

Why the greatest common divisor of m and n always divides the number of filled squares?