Space filling curve
Published:
In this post I would like to share my old writeup about there existence of a continuous surjective map from $\mathbb{R}$ to $\mathbb{R}^2$. In other words, we will prove that that Hilbert’s Curve is a continuous surjective map. The proof presented here was explained by Dr. Manas Ranjan Sahoo, 3 years ago on 15th April 2016.
Consider $f : \mathbb{R} \rightarrow [0,1]$
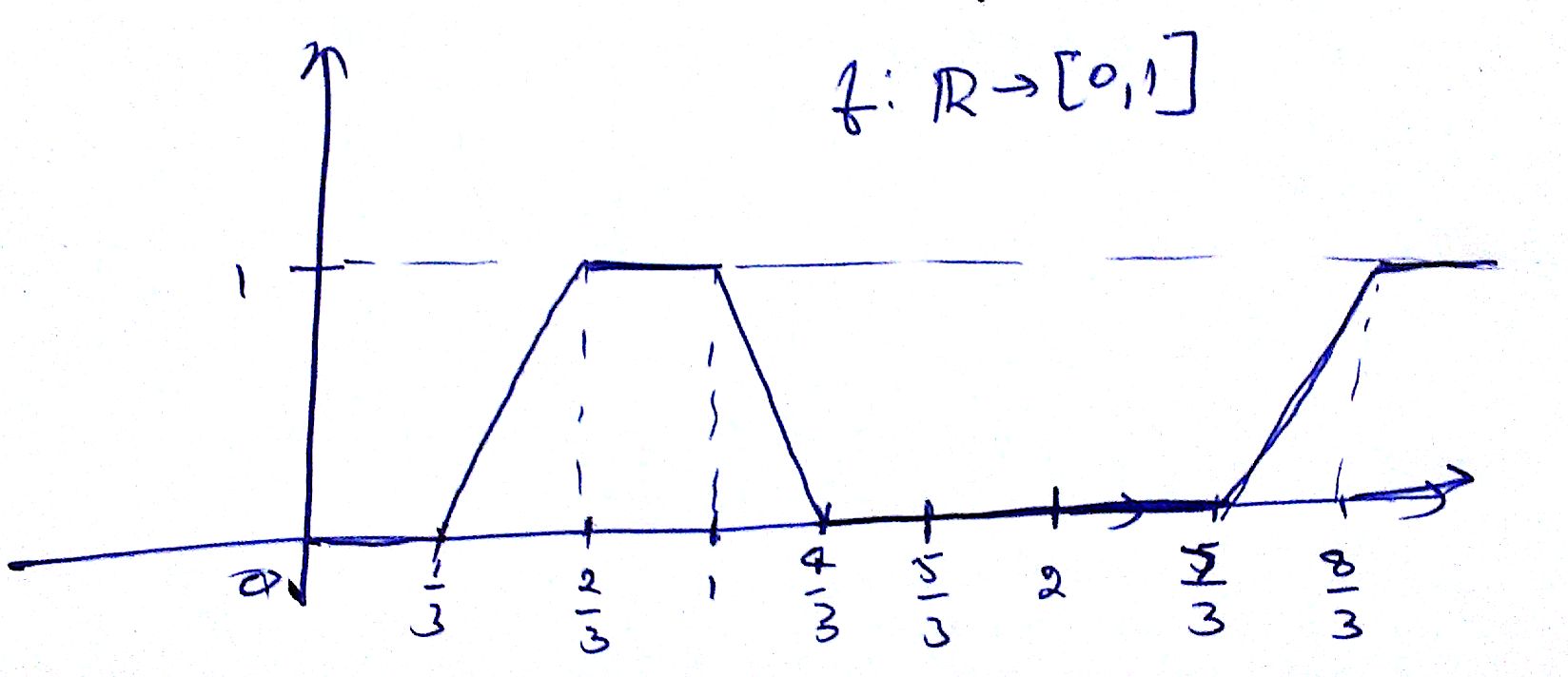
Observe that $f$ is a continuous periodic function with period 2. Hence, $f(x+2I) = f(x)$ for any integer $I$.
Now consider, $g : [0,1] \rightarrow [0,1]\times [0,1]$ where $g(t) = \left(x(t), y(t)\right)$. We define the map $g$ as:
\[\begin{cases} x(t) = \frac{1}{2}f(t) + \frac{1}{2^2}f(3^2t) + \frac{1}{2^3} f(3^4 t) + \ldots = \displaystyle{\sum_{n=0}^{\infty} \frac{1}{2^{n+1}} f\left(3^{2n}t\right)}\\ y(t) = \frac{1}{2}f(3t) + \frac{1}{2^2}f(3^3t) + \frac{1}{2^5} f(3^4 t) + \ldots = \displaystyle{\sum_{n=0}^{\infty} \frac{1}{2^{n+1}} f\left(3^{2n+1}t\right)} \end{cases}\]Now this map is continuous from Weierstrass M-test, which states that:
Suppose that $\{f_n\}$ is a sequence of real or complex-valued functions defined on a set $A$, and that there is a sequence of positive numbers $\{M_n\}$ satisfying \[\forall n \geq 1, \forall x \in A: \ |f_n(x)|\leq M_n \nonumber\] \[\sum_{n=1}^{\infty} M_n < \infty \nonumber \] Then the series \[\sum_{n=1}^{\infty} f_n (x) \nonumber \] converges uniformly on $A$.
Thus, $g$ is continuous because $f$ is continuous.
Now we will prove that $g$ is surjective, that is, for all $(x_0, y_0)$ in $[0,1]\times [0,1]$ there exist $t_0$ in $[0,1]$ such that $x(t_0) = x_0$ and $y(t_0) = y_0$.
Trick: Represent the elements $t_0$ in ternary and $x_0, y_0$ in binary.
Hence we can write:
\[\begin{cases} x_0 = 0.a_0a_2a_4a_6\ldots = \displaystyle{\sum_{i=0}^{\infty} \frac{1}{2^{i+1}}a_{2i}}\\ y_0 = 0.a_1a_3a_5a_7\ldots = \displaystyle{\sum_{i=0}^{\infty} \frac{1}{2^{i+1}}a_{2i+1}} \end{cases}\]where $a_i \in \{0,1\}$ for all $i$. Also,
\[t_0 = 0.(2a_0)(2a_1)(2a_2)\ldots = \displaystyle{\sum_{i=0}^{\infty} \frac{1}{3^{i+1}}2a_{i}}\]where $(2a_i) \in \{0,2\}$ for all $i$ (motivating the idea of representing $t_0$ in ternary)
Claim: $x(t_0) = x_0$ and $y(t_0) = y_0$
Using the ternary expansion of $t_0$ we will get
\[\begin{eqnarray*} 3^n t_0 & = & 3^n \left(\sum_{i=0}^{\infty} \frac{2a_i}{3^{i+1}}\right) \\ &=& 3^n \left(\sum_{i=0}^{n-1} \frac{2a_i}{3^{i+1}} + \sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}}\right) \\ &=& 2I + 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}} \end{eqnarray*}\]
where $\displaystyle{3^n\sum_{i=0}^{n-1} \frac{2a_i}{3^{i+1}}}$ is twice an integer since $3^n \geq 3^{i+1}$ for $0\leq i \leq n-1$ (hence we could take 2 out of summation).
Now $a_n$ can be either 0 or 1. We will consider following two cases:
- $a_n = 0$ \[\begin{eqnarray*} 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}} & = & 3^n\sum_{i=n+1}^{\infty} \frac{2a_i}{3^{i+1}} \\ &\leq & 3^n\sum_{i=n}^{\infty} \frac{2}{3^{i+1}} \qquad \text{(substitute maximum value of $a_i$)}\\ & = & \frac{1}{3} \qquad \text{(sum of infinite geometric progression)} \end{eqnarray*}\] Also observe that if we substitute minimum value of $a_i$ we will get $0 \leq 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}}$, hence \[0 \leq 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}} \leq \frac{1}{3} \nonumber\] \[\Rightarrow f\left(2I+ 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}}\right) = 0 \nonumber\] from the definition of $f$ given in the starting.
- $a_n = 1$ \[\begin{eqnarray*} 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}} & = & \frac{2}{3} + 3^n\sum_{i=n+1}^{\infty} \frac{2a_i}{3^{i+1}} \\ &\leq & \frac{2}{3} + 3^n\sum_{i=n}^{\infty} \frac{2}{3^{i+1}} \qquad \text{(substitute maximum value of $a_i$)}\\ & = & \frac{2}{3} + \frac{1}{3} \qquad \text{(sum of infinite geometric progression)}\\ &=& 1 \end{eqnarray*}\] Also observe that if we substitute minimum value of $a_i$ we will get $\frac{2}{3}+0 \leq 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}}$, hence \[\frac{2}{3} \leq 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}} \leq 1 \nonumber \] \[\Rightarrow f\left(2I+ 3^n\sum_{i=n}^{\infty} \frac{2a_i}{3^{i+1}}\right) = 1 \nonumber\] from the definition of $f$ given in the starting.
Now combining both the above cases we conclude that:
\[f(3^n t_0) = a_n\]Hence:
\[\begin{cases} x(t_0) = \displaystyle{\sum_{n=0}^{\infty} \frac{1}{2^{n+1}} f\left(3^{2n}t_0\right) = \sum_{n=0}^{\infty} \frac{1}{2^{n+1}}a_{2n}} = x_0\\ y(t_0) = \displaystyle{\sum_{n=0}^{\infty} \frac{1}{2^{n+1}} f\left(3^{2n+1}t_0\right) = \sum_{n=0}^{\infty} \frac{1}{2^{n+1}}a_{2n+1}} = y_0 \end{cases}\]Thus proving our claim. Therefore, $g$ is surjective.
From standard exercises in metric spaces we know that $[0,1]$ is homeomorphic to $\mathbb{R}$ and $[0,1]\times [0,1]$ is homeomorphic to $\mathbb{R}^2$.
Let $\phi : \mathbb{R} \rightarrow [0,1]$ and $\psi : [0,1]\times [0,1] \rightarrow \mathbb{R}^2$ be the homeomorphisms, then

Thus the composition, $\Gamma = \psi \circ g \circ \phi$ is the required continuous surjective map.
Exercise: Verify that the function $\Gamma : \mathbb{R} \rightarrow \mathbb{R}^2$ defined above will give Hilbert's Curve.
