Bicylinder: Steinmetz solid

Consider the following example from Piskunov’s “Integral and Differential Calculus”:

Find the area of that part of the surface of the cylinder $x^2+y^2=a^2$ which is cut out by the cylinder $x^2+z^2=a^2$.

Here we need to find the surface area $S$ of the part of cylinder $C_1: x^2+y^2=a^2$ which lies inside the cylinder $C_2: x^2+z^2=a^2$. That is, the surface $S$ is bounded by the curve $\Gamma$ traced at the intersection of the two curves.

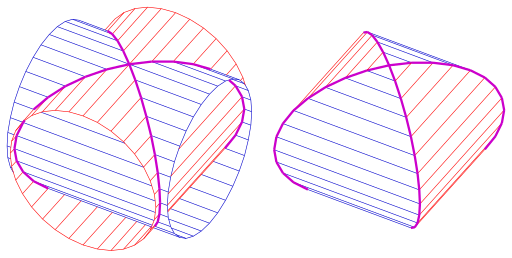
The projection of $\Gamma$ in the $xz$-plane gvies us the domain $D: \{x^2+z^2\leq a^2\}$. Next we consider the part of desired surface in the first octant, and use the following surface area formula:

$ \displaystyle{\frac{1}{8}S = \iint_{D'} \sqrt{1+\left(\frac{\partial f}{\partial x}\right)^2 + \left(\frac{\partial f}{\partial z}\right)^2}dz dx}$

where $f(x,z)= y = \sqrt{a^2-x^2}$ and $D’ = \{(x,z)\in D : x,z\geq 0\} $. Therefore, we have

$\displaystyle{\frac{1}{8}S = \int_{0}^a \int_{0}^{\sqrt{a^2-x^2}}\sqrt{1+ \left(-\frac{x}{\sqrt{a^2-x^2}}\right)^2 + \left(0\right)^2}dz dx }$

$\displaystyle{= \int_{0}^a \int_{0}^{\sqrt{a^2-x^2}}\frac{a}{\sqrt{a^2-x^2}}dz dx = a \int_0^a \left[\frac{z}{\sqrt{a^2-x^2}}\right]_0^{\sqrt{a^2-x^2}}dx}$

$\displaystyle{= a\int_0^1 dx = a^2}$

(luckily we don’t need change of variables!)

Hence, $\boxed{S = 8a^2}$. I found this problem to be visually challenging, though the surface area and volume follow directly from the general formulas.