Gaurish Korpal

Gaurish Korpal

PhD Candidate

Good Articles

Published:

Following are some of the mathematics articles that I would recommend reading. The inspiration for this list came from the anthologies like Who Gave You the Epsilon? And Other Tales of Mathematical History and Biscuits of Number Theory.

Here I have divided articles between applied mathematics (computational mathematics) and pure mathematics (algebra and number theory). Loosely speaking, computer science is a specialization within the discipline of computational mathematics (not to be confused with computational science), and computer engineering is a specialization within the discipline of electrical engineering (closely related to physics and applied mathematics), for details see this 1989 report by the ACM Education Board. Moreover, I believe in the exsitence of the following hierarchy in STEM fields, i.e. outer one assumes results from the inner ones, illustrated alongside using elliptic curve cryptography:

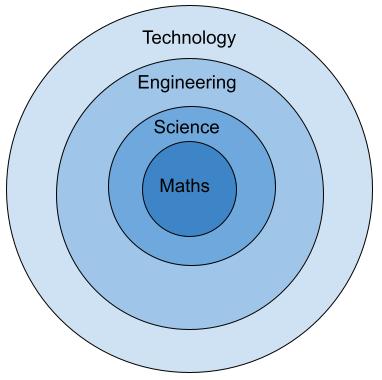
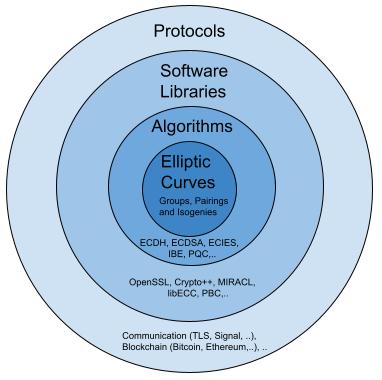
STEM crypt

Note that the order of authors’ names in pure mathematics and applied mathematics (similar to science and engineering) articles tend to have a different meaning, for details see this 1992 paper by Andrew Appel and this 2004 statement by the AMS.

One might need university library membership to access some of these articles (or use the power of internet). I have arranged the articles in reverse chronological order (from the latest to the oldest).

Applied Mathematics

Expository

  • A. Menezes and D. Stebila, Challenges in Cryptography, IEEE Security & Privacy 19 (2021), no. 2, 70–73. doi:10.1109/MSEC.2021.3049730
  • P. C. van Oorschot, Toward Unseating the Unsafe C Programming Language, IEEE Security & Privacy 19 (2021), no. 2, 4–6. doi:10.1109/MSEC.2020.3048766
  • T. Lindell, Secure multiparty computation, Communications of the ACM 64 (2021), no. 1, 86–96. doi:10.1145/3387108, Stable URL
  • C. Peng, J. Chen, S. Zeadally and D. He, Isogeny-Based Cryptography: A Promising Post-Quantum Technique, IEEE IT Professional 21 (2019), no. 6, 27–32. doi:10.1109/MITP.2019.2943136 [Contains nice illustrations.]
  • C. Martindale and L. Panny, Isogeny-based cryptography, Computeralgebra-Rundbrief (Computer Algebra Newsletter) 65 (2019), no. 1, 12–17. Stable URL, preprint [Contains nice illustrations.]
  • J. Waldo, A Hitchhiker’s Guide to the Blockchain Universe: Blockchain remains a mystery, despite its growing acceptance, ACM Queue 16 (2018), no. 6, 15 pp. doi:10.1145/3305263.3305265, Stable URL
  • A. Narayanan and J. Clark, Bitcoin’s Academic Pedigree: The concept of cryptocurrencies is built from forgotten ideas in research literature, ACM Queue 15 (2017), no. 4, 30 pp. doi:10.1145/3134434.3136559, Stable URL [An equivalent quality video exposition by Grant Sanderson (3Blue1Brown) on YouTube]
  • K. Lauter, Postquantum Opportunities: Lattices, Homomorphic Encryption, and Supersingular Isogeny Graphs, IEEE Security & Privacy 15 (2017), no. 4, 22–27. doi:10.1109/MSP.2017.3151338
  • H. Cohn, A conceptual breakthrough in sphere packing, Notices Amer. Math. Soc. 64 (2017), no. 2, 102–115. doi:10.1090/noti1474
  • N. Koblitz and A. Menezes, A Riddle Wrapped in an Enigma, IEEE Security & Privacy 14 (2016), no. 6, 34–42. doi:10.1109/MSP.2016.120 [There are equivalent quality video expositions by Numberphile (2013) and Computerphile (2018)]
  • N. Koblitz and A. Menezes, Cryptocash, cryptocurrencies, and cryptocontracts, Designs, Codes and Cryptography 78 (2016), no. 1, 87–102. doi:10.1007/s10623-015-0148-5
  • J. Bonneau, A. Miller, J. Clark, A. Narayanan, J. A. Kroll and E. W. Felten, SoK: Research Perspectives and Challenges for Bitcoin and Cryptocurrencies, Proc. of S&P (Oakland) 2015. doi: 10.1109/SP.2015.14.
  • S. Kamara, Encrypted Search, XRDS: Crossroads, The ACM Magazine for Students 21 (2015), no. 3, 30–34. doi:10.1145/2730908, Stable URL
  • D. Boneh, A. Sahai and B. Waters, Functional encryption: a new vision for public-key cryptography, Communications of the ACM 55 (2012), no. 11, 56–64. doi:10.1145/2366316.2366333, Stable URL
  • C. P. Pfleeger, Crypto: Not Just for the Defensive Team, IEEE Security & Privacy 8 (2010), no. 2, 63–66. doi:10.1109/MSP.2010.65
  • C. Christensen, Polish Mathematicians Finding Patterns in Enigma Messages, Math. Mag. 80 (2007), no. 4, 247–273. Stable URL
  • R. Gennaro, Randomness in cryptography, IEEE Security & Privacy 4 (2006), no. 2, 64–67. doi:10.1109/MSP.2006.49
  • K. Lauter, The advantages of elliptic curve cryptography for wireless security, IEEE Wireless Communications 11 (2004), no. 1, 62–67. doi:10.1109/MWC.2004.1269719
  • B. Schneier, Cryptography: the importance of not being different, IEEE Computer 32 (1999), no. 3, 108–109. doi:10.1109/2.751335
  • N. Koblitz, Cryptography as a teaching tool, Cryptologia 21 (1997), no. 4, 317–326. doi:10.1080/0161-119791885959

Research

  • R. Wang, Y. Shoshitaishvili, C. Kruegel, and G. Vigna, Steal This Movie: Automatically Bypassing DRM Protection in Streaming Media Services, USENIX 13. Stable link
  • D. Boneh and M. Franklin, Identity-Based Encryption from the Weil Pairing, Proc. of Crypto 2001. doi:10.1007/3-540-44647-8_13 [The full version of this paper was published in SICOMP 32 (2003), no. 3. doi:10.1137/S0097539701398521 ]
  • M. Fellows and N. Koblitz, Kid Krypto, Proc. of Crypto 1992. doi:10.1007/3-540-48071-4_27
  • D. Chaum and E. van Heyst, Group Signatures, Proc. of Eurocrypt 1991. doi:10.1007/3-540-46416-6_22
  • N. Koblitz, Elliptic curve cryptosystems. Math. Comp. 48 (1987), no. 177, 203–209. doi:10.2307/2007884
  • V. S. Miller, Use of Elliptic Curves in Cryptography, Proc. of Crypto 1985. doi:10.1007/3-540-39799-X_31
  • A. Shamir, Identity-Based Cryptosystems and Signature Schemes, Proc. of IACR Crypto 1984. doi:10.1007/3-540-39568-7_5
  • A. C. Yao, Protocols for secure computations, Proc. of IEEE Symp. on FOCS 1982. doi:10.1109/SFCS.1982.38
  • M. Rejewski, An Application of the Theory of Permutations in Breaking the Enigma Cipher, Zastos. Mat. [Appl. Math. (Warsaw)], 16 (1980), no. 4, 543–559. doi:10.4064/am-16-4-543-559

As one can see, my knowledge of computer science is limited to cryptography. Note that the key theoretical cryptography results are generally announced in the conferences like Crypto, Eurocrypt, Asiacrypt, TCC, FOCS, STOC, ANTS, and AGC2T. On the other hand, the key applied cryptography results are generally announced in the conferences like S&P (Oakland), CCS, CHES, and USENIX Security. A more comprehensive list of relevant conferences can be found here.

Pure Mathematics

Expository

  • J. S. Chahal, What Do Networks and Elliptic Curves Have in Common?, Amer. Math. Monthly 130 (2023), no. 2, 158-175, doi:10.1080/00029890.2022.2141548
  • W. D’Alessandro, Proving quadratic reciprocity: explanation, disagreement, transparency and depth, Synthese 198 (2021), 8621–8664. doi:10.1007/s11229-020-02591-6
  • F. Oort, The Weil Conjectures, Nieuw Arch. Wiskd. (5) 15 (2014), no. 6, 211–219. Stable URL (There is a calculation error in the last line of the middle column of p. 214, $\alpha^{10},\beta^{10} = \mp 32i$).
  • C. S. Dalawat, Classical Reciprocity Laws, Asia Pac. Math. Newsl. 4 (2014), no. 4, 5–9. Stable URL
  • F. Oort, Prime Numbers, ICCM Not. 1 (2013), no. 2, 60–78. doi:10.4310/ICCM.2013.v1.n2.a8
  • U. A. Rozikov, What are p-adic Numbers? What are they used for?, Asia Pac. Math. Newsl. 3 (2013), no. 4, 1–6. Stable URL
  • R. Sreekantan, Yitang Zhang and The Twin Primes Conjecture, At Right Angles 2 (2013), no. 3, 14–17. Stable URL
  • A. Rice and E. Brown, Why Ellipses Are Not Elliptic Curves, Math. Mag. 85 (2012), no. 3, 163–176. doi:10.4169/math.mag.85.3.163, Stable URL
  • B. Sury, Nothing lucky about 13, Math. Mag. 83 (2010), no. 4, 289–293. doi:10.4169/002557010X521840
  • G. Frey, The Arithmetic Behind Cryptography, Notices Amer. Math. Soc. 57 (2010), no. 3, 366–374. Stable URL
  • F. Morgan, Fermat’s last theorem for fractional and irrational exponents, College Math. J. 41 (2010), no. 3, 182–185. doi:10.4169/074683410X488647
  • J. DeMaio and A. Lightcap, A Graph Theoretic Summation of the Cubes of the First $n$ Integers, Math. Mag. 82 (2009), no. 5, 363–364. doi:10.4169/002557009X478409
  • J. B. Gil and M. D. Weiner, A Quick Change of Base Algorithm for Fractions, College Math. J. 39 (2008), no. 1, 56–59. Stable URL
  • W. Y. Pong, Sums of consecutive integers, College Math. J. 38 (2007), no. 2, 119–123. doi:10.1080/07468342.2007.11922226
  • A. Granville and G. Martin, Prime Number Races, Amer. Math. Monthly 113 (2006), no. 1, 1–33. Stable URL
  • G. Garza and J. Young, Wieferich Primes and Period Lengths for the Expansions of Fractions, Math. Mag. 77 (2004), no. 4, 314–319. Stable URL
  • D. Khurana, On GCD and LCM in Domains – A Conjecture of Gauss, Resonance 8 (2003), no. 6, 72–79. Stable URL
  • J. B. Conrey, The Riemann Hypothesis, Notices Amer. Math. Soc. 50 (2003), no. 3, 341–353. Stable URL
  • S. Ahlgren and K. Ono, Adding and counting: The arithmetic of partitions, Notices Amer. Math. Soc. 48 (2001), no. 9, 978–984. Stable URL
  • G. P. Dresden, Two Irrational Numbers from the Last Nonzero Digits of $n!$ and $n^n$, Math. Mag. 74 (2001), no. 4, 316–320. Stable URL
  • B. Sury, Cyclotomy and Cyclotomic Polynomials - The Story of how Gauss Narrowly Missed Becoming a Philologist, Resonance 4 (1999), no. 12, 41–53. Stable URL
  • W. D. Stangl, Counting squares in Zn, Math. Mag. 69 (1996), no. 4, 285–289. Stable URL
  • P. Stevenhagen and H. W. Lenstra, Chebotarëv and his Density Theorem, Math. Intelligencer 18 (1996), no. 2, 26–37. doi:10.1007/BF03027290
  • N. Schappacher and R. Schoof, Beppo Levi and the arithmetic of elliptic curves, Math. Intelligencer 18 (1996), no. 1, 57–69. doi:10.1007/BF03024818
  • J. Shallit, Origins of the analysis of the Euclidean algorithm, Historia Mathematica 21 (1994), no. 4, 401–419. doi:10.1006/hmat.1994.1031
  • D. E. G. Malm, A graph of primes, Math. Mag. 66 (1993), no. 5, 317–320. Stable URL
  • E. Bombieri, Prime Territory, The Sciences 32 (1992), no. 5, 30–36. doi:10.1002/j.2326-1951.1992.tb02416.x
  • A. D. Abrams and M. J. Paris, The Probability that $(a,b) = 1$, College Math. J. 23 (1992), no. 1, 47. Stable URL
  • B. Mazur, Number theory as gadfly, Amer. Math. Monthly 98 (1991), no. 7, 593–610. Stable URL
  • G. P. Graham and C. E. Roberts, A Diophantine equation from calculus, Math. Mag. 62 (1989), no. 2, 97–101. doi:10.1080/0025570X.1989.11977418, Stable URL
  • F. Bien, Constructions of telephone networks by group representations, Notices Amer. Math. Soc. 36 (1989), no. 1, 5–22. Stable URL
  • D. Castellanos, The Ubiquitous $\pi$ (Part 2). Math. Mag. 61 (1988), no. 3, 148–163. Stable URL (also see the Wolfram article containging illustration of GCD lattices)
  • D. Castellanos, The Ubiquitous $\pi$ (Part 1). Math. Mag. 61 (1988), no. 2, 67–98.Stable URL
  • M. Ram Murty, Artin’s conjecture for primitive roots, Math. Intelligencer 10 (1988), no. 1, 59–67. doi:10.1007/BF03023749
  • J. T. Cross, Primitive Pythagorean triples of Gaussian integers, Math. Mag. 59 (1986), no. 2, 106–110. Stable URL
  • S. Bloch, The proof of the mordell conjecture, Math. Intelligencer 6 (1984), no. 1, 41–47. doi:10.1007/BF03024155
  • N. Koblitz, Why study equations over finite fields?, Math. Mag. 55 (1982), no. 3, 144–149. doi:10.2307/2690080, Stable URL
  • M. Rosen, Abel’s Theorem on the Lemniscate, Amer. Math. Monthly 88 (1981), no. 6, 387–395. Stable URL
  • H. M. Edwards, Fermat’s Last Theorem, Scientific American 239 (1978), no. 4, 104–-122. doi: 10.1038/scientificamerican1078-104, Stable URL
  • D. Zagier, The first 50 million prime numbers, Math. Intelligencer 1 (1977), no. 1, 7–19. doi:10.1007/BF03039306
  • B. L. van der Waerden, Hamilton’s Discovery of Quaternions, Math. Mag. 49 (1976), no. 5, 227–234. doi:10.2307/2689449, Stable URL
  • M. Davis and R. Hersh, Hilbert’s 10th Problem, Scientific American 229 (1973), no. 5, 84–91. doi: 10.1038/scientificamerican1173-84, Stable URL
  • G. H. Hardy, An introduction to the theory of numbers, Bull. Amer. Math. Soc. 35 (1929), no. 6, 778–818. doi:10.1090/S0002-9904-1929-04793-1

I have fond memories of reading expository articles in Indian magazines like Junior Mathematician (published by AMTI, Chennai) and Bona Mathematica (published by BP, Pune), which were similar to the Soviet era periodicals like Kvant (published by Nauka; english translations published in Quantum and AMS) and Little Mathematics Library (english translations published by Mir). Unfortunately, they are not available online (but were accessible without university library membership). Fortunately, At Right Angles (supported by APU, Bengaluru), Resonance (supported by IAS, Bengaluru), Bhavana (supported by an independent trust), Pi in the Sky (supported by PIMS), Crux Mathematicorum (supported by CMS, Ottawa), Mathematical Reflections (supported by AwesomeMath.org), Chalkdust (supported by the UK universities), and Plus (supported by the University of Cambridge) are great free alternatives available online.

The Mathematical Association of America (MAA) publishes many exposition focused journals like the American Mathematical Monthly, Mathematics Magazine, the College Mathematics Journal and Math Horizons, but they are behind paywalls (in India I was only able to access the archives available via JSTOR and Classroom Capsules). Similarly, the Mathematical Association publishes The Mathematical Gazette, SYMmetry Plus etc. Other paid expository periodicals are Mathematical Intelligencer and Rocky Mountain Journal of Mathematics. Moreover, the Princeton Companion to Mathematics contains many original expository articles about almost every topic in maths.

Research

  • A. Granville, Squares in Arithmetic Progressions and Infinitely Many Primes, Amer. Math. Monthly 124 (2017), no. 10, 951–954. doi:10.4169/amer.math.monthly.124.10.951, Stable URL
  • J. A. Zuehlke, Fermat’s last theorem for Gaussian integer exponents, Amer. Math. Monthly 106 (1999), no. 1, 49. doi:10.1080/00029890.1999.12005006
  • A. P. Ogg, Automorphismes de courbes modulaires. Séminaire Delange-Pisot-Poitou 16 (1975) no. 1, 8 p. Stable URL
  • J. E. Nymann, On the probability that $k$ positive integers are relatively prime. II. J. Number Theory 7 (1975), no. 4, 406–-412. doi:10.1016/0022-314X(75)90044-X
  • J. E. Nymann, On the probability that $k$ positive integers are relatively prime. J. Number Theory 4 (1972), 469–473. doi:10.1016/0022-314X(72)90038-8 (also see this blog post)
  • H. M. Stark, A complete determination of the complex quadratic fields of class-number one, Michigan Math. J. 14 (1967), no. 1, 1–27, doi:10.1307/mmj/1028999653
  • K. F. Roth, Rational approximations to algebraic numbers, Mathematika 2 (1955), no. 1, 1–20. doi:10.1112/S0025579300000644
  • I. Niven, A simple proof that $\pi$ is irrational, Bull. Amer. Math. Soc. 53 (1947), no. 6, 509–509. Stable URL (this method was later generalized by A. E. Parks)